SO(3) matrix

class SO3(*args, **kwargs)[source]

Bases: BasePoseMatrix

SO(3) matrix class

This subclass represents rotations in 3D space. Internally it is a 3x3 orthogonal matrix belonging to the group SO(3).

Inheritance diagram of spatialmath.pose3d.SO3
classmethod Alloc(n=1)

Construct an instance with N default values (BasePoseList superclass method)

Parameters:

n (int, optional) – Number of values, defaults to 1

Return type:

Self

Returns:

pose instance with n default values

X.Alloc(N) creates an instance of the pose class X with N default values, ie. len(X) will be N.

X can be considered a vector of pose objects, and those elements can be referenced X[i] or assigned to X[i] = ....

Note

The default value depends on the pose class and is the result of the empty constructor. For SO2, SE2, SO3, SE3 it is an identity matrix, for a twist class Twist2 or Twist3 it is a zero vector, for a UnitQuaternion or Quaternion it is a zero vector.

Example:

>>> x = X.Alloc(10)
>>> len(x)
10

where X is any of the SMTB classes.

classmethod AngVec(theta, v, *, unit='rad')[source]

Construct a new SO(3) rotation matrix from rotation angle and axis

Parameters:

  • theta (float) – rotation

  • unit (str) – angular units: ‘rad’ [default], or ‘deg’

  • v (array_like) – rotation axis, 3-vector

Returns:

SO(3) rotation

Return type:

SO3 instance

SO3.AngVec(theta, V) is an SO(3) rotation defined by a rotation of THETA about the vector V.

Deprecated since version 0.9.8: Use AngleAxis() instead.

Seealso:

angvec(), spatialmath.base.transforms3d.angvec2r()

classmethod AngleAxis(theta, v, *, unit='rad')[source]

Construct a new SO(3) rotation matrix from rotation angle and axis

Parameters:

  • theta (float) – rotation

  • unit (str) – angular units: ‘rad’ [default], or ‘deg’

  • v (array_like) – rotation axis, 3-vector

Returns:

SO(3) rotation

Return type:

SO3 instance

SO3.AngleAxis(theta, V) is an SO(3) rotation defined by a rotation of THETA about the vector V.

Note

\(\theta \eq 0\) the result in an identity matrix, otherwise V must have a finite length, ie. \(|V| > 0\).

Seealso:

angvec(), spatialmath.base.transforms3d.angvec2r()

classmethod Empty()

Construct an empty instance (BasePoseList superclass method)

Return type:

Self

Returns:

pose instance with zero values

Example:

>>> x = X.Empty()
>>> len(x)
0

where X is any of the SMTB classes.

classmethod Eul(*angles, unit='rad')[source]

Construct a new SO(3) from Euler angles

Parameters:

  • 𝚪 (3 floats, array_like(3) or ndarray(N,3)) – Euler angles

  • unit (str) – angular units: ‘rad’ [default], or ‘deg’

Returns:

SO(3) rotation

Return type:

SO3 instance

SO3.Eul(𝚪) is an SO(3) rotation defined by a 3-vector of Euler

angles \(\Gamma = (\phi, \theta, \psi)\) which correspond to consecutive rotations about the Z, Y, Z axes respectively. If 𝚪 is an Nx3 matrix then the result is a sequence of rotations each defined by Euler angles corresponding to the rows of angles.

SO3.Eul(φ, θ, ψ) as above but the angles are provided as three

scalars.

Example:

>>> from spatialmath import SO3
>>> SO3.Eul(0.1, 0.2, 0.3)
SO3(array([[ 0.9021, -0.3836,  0.1977],
           [ 0.3875,  0.9216,  0.0198],
           [-0.1898,  0.0587,  0.9801]]))
>>> SO3.Eul([0.1, 0.2, 0.3])
SO3(array([[ 0.9021, -0.3836,  0.1977],
           [ 0.3875,  0.9216,  0.0198],
           [-0.1898,  0.0587,  0.9801]]))
>>> SO3.Eul(10, 20, 30, unit="deg")
SO3(array([[ 0.7146, -0.6131,  0.3368],
           [ 0.6337,  0.7713,  0.0594],
           [-0.2962,  0.171 ,  0.9397]]))
Seealso:

eul(), Eul(), eul2r()

classmethod EulerVec(w)[source]

Construct a new SO(3) rotation matrix from an Euler rotation vector

Parameters:

ω (3-element array_like) – rotation axis

Returns:

SO(3) rotation

Return type:

SO3 instance

SO3.EulerVec(ω) is a unit quaternion that describes the 3D rotation defined by a rotation of \(\theta = \lVert \omega \rVert\) about the unit 3-vector \(\omega / \lVert \omega \rVert\).

Example:

>>> from spatialmath import SO3
>>> SO3.EulerVec([0.5,0,0])
SO3(array([[ 1.    ,  0.    ,  0.    ],
           [ 0.    ,  0.8776, -0.4794],
           [ 0.    ,  0.4794,  0.8776]]))

Note

\(\theta \eq 0\) the result in an identity matrix, otherwise V must have a finite length, ie. \(|V| > 0\).

Seealso:

angvec(), angvec2r()

classmethod Exp(S, check=True, so3=True)[source]

Create an SO(3) rotation matrix from so(3)

Parameters:

  • S (ndarray(3,3), ndarray(n,3)) – Lie algebra so(3)

  • check (bool) – check that passed matrix is valid so(3), default True

  • so3 (bool) – the input is interpretted as an so(3) matrix not a stack of three twists, default True

Bool check:

bool, optional

Returns:

SO(3) rotation

Return type:

SO3 instance

  • SO3.Exp(S) is an SO(3) rotation defined by its Lie algebra which is a 3x3 so(3) matrix (skew symmetric)

  • SO3.Exp(t) is an SO(3) rotation defined by a 3-element twist vector (the unique elements of the so(3) skew-symmetric matrix)

  • SO3.Exp(T) is a sequence of SO(3) rotations defined by an Nx3 matrix of twist vectors, one per row.

  • if \(\theta \eq 0\) the result in an identity matrix

  • an input 3x3 matrix is ambiguous, it could be the first or third case above. In this case the parameter so3 is the decider.

Seealso:

spatialmath.base.transforms3d.trexp(), spatialmath.base.transformsNd.skew()

classmethod OA(o, a)[source]

Construct a new SO(3) from two vectors

Parameters:

  • o (array_like) – 3-vector parallel to Y- axis

  • a (Union[List, Tuple[float, float, float], ndarray[Any, dtype[TypeVar(ScalarType, bound= generic, covariant=True)]]]) – 3-vector parallel to the Z-axis

Returns:

SO(3) rotation

Return type:

SO3 instance

SO3.OA(O, A) is an SO(3) rotation defined in terms of vectors parallel to the Y- and Z-axes of its reference frame. In robotics these axes are respectively called the orientation and approach vectors defined such that R = [N, O, A] and N = O x A.

Note

  • Only the A vector is guaranteed to have the same direction in the resulting

rotation matrix - O and A do not have to be unit-length, they are normalized - O and ``A` do not have to be orthogonal, so long as they are not parallel

Seealso:

spatialmath.base.transforms3d.oa2r()

classmethod RPY(*angles, unit='rad', order='zyx')[source]

Construct a new SO(3) from roll-pitch-yaw angles

Parameters:

  • angles (array_like(3), array_like(n,3)) – roll-pitch-yaw angles

  • unit (str) – angular units: ‘rad’ [default], or ‘deg’

  • order (str) – rotation order: ‘zyx’ [default], ‘xyz’, or ‘yxz’

Returns:

SO(3) rotation

Return type:

SO3 instance

  • SO3.RPY(angles) is an SO(3) rotation defined by a 3-vector of roll, pitch, yaw angles \((\alpha, \beta, \gamma)\). If angles is an Nx3 matrix then the result is a sequence of rotations each defined by RPY angles corresponding to the rows of angles. The angles correspond to successive rotations about the axes specified by order:

    • 'zyx' [default], rotate by yaw about the z-axis, then by pitch about the new y-axis, then by roll about the new x-axis. Convention for a mobile robot with x-axis forward and y-axis sideways.

    • 'xyz', rotate by yaw about the x-axis, then by pitch about the new y-axis, then by roll about the new z-axis. Convention for a robot gripper with z-axis forward and y-axis between the gripper fingers.

    • 'yxz', rotate by yaw about the y-axis, then by pitch about the new x-axis, then by roll about the new z-axis. Convention for a camera with z-axis parallel to the optic axis and x-axis parallel to the pixel rows.

  • SO3.RPY(⍺, β, 𝛾) as above but the angles are provided as three scalars.

Example:

>>> from spatialmath import SO3
>>> SO3.RPY(0.1, 0.2, 0.3)
SO3(array([[ 0.9363, -0.2751,  0.2184],
           [ 0.2896,  0.9564, -0.037 ],
           [-0.1987,  0.0978,  0.9752]]))
>>> SO3.RPY([0.1, 0.2, 0.3])
SO3(array([[ 0.9363, -0.2751,  0.2184],
           [ 0.2896,  0.9564, -0.037 ],
           [-0.1987,  0.0978,  0.9752]]))
>>> SO3.RPY(0.1, 0.2, 0.3, order='xyz')
SO3(array([[ 0.9752, -0.0978,  0.1987],
           [ 0.1538,  0.9447, -0.2896],
           [-0.1593,  0.313 ,  0.9363]]))
>>> SO3.RPY(10, 20, 30, unit="deg")
SO3(array([[ 0.8138, -0.441 ,  0.3785],
           [ 0.4698,  0.8826,  0.018 ],
           [-0.342 ,  0.1632,  0.9254]]))
Seealso:

rpy(), RPY(), spatialmath.base.transforms3d.rpy2r()

classmethod Rand(N=1, *, theta_range=None, unit='rad')[source]

Construct a new SO(3) from random rotation

Parameters:

  • N (int) – number of random rotations

  • theta_range (Union[List, Tuple[float, float], ndarray[Any, dtype[TypeVar(ScalarType, bound= generic, covariant=True)]], None]) – angular magnitude range [min,max], defaults to None.

  • unit (str) – angular units: ‘rad’ [default], or ‘deg’

Returns:

SO(3) rotation matrix

Return type:

SO3 instance

  • SO3.Rand() is a random SO(3) rotation.

  • SO3.Rand(N) is a sequence of N random rotations.

Example:

>>> from spatialmath import SO3
>>> x = SO3.Rand()
>>> x
SO3(array([[-0.7756, -0.5699, -0.2715],
           [ 0.3374, -0.0106, -0.9413],
           [ 0.5336, -0.8216,  0.2005]]))
Seealso:

spatialmath.quaternion.UnitQuaternion.Rand()

classmethod RotatedVector(v1, v2, tol=20)[source]

Construct a new SO(3) from a vector and its rotated image

Parameters:

  • v1 (array_like(3)) – initial vector

  • v2 (array_like(3)) – vector after rotation

  • tol (float) – tolerance for singularity in units of eps, defaults to 20

Returns:

SO(3) rotation

Return type:

SO3 instance

SO3.RotatedVector(v1, v2) is an SO(3) rotation defined in terms of two vectors. The rotation takes vector v1 to v2.

>>> from spatialmath import SO3
>>> v1 = [1, 2, 3]
>>> v2 = SO3.Eul(0.3, 0.4, 0.5) * v1
>>> print(v2)
[[0.3842]
 [2.4579]
 [2.7948]]
>>> R = SO3.RotatedVector(v1, v2)
>>> print(R)
   0.9857   -0.1131   -0.1251    
   0.1282    0.9844    0.1203    
   0.1095   -0.1346    0.9848    

>>> print(R * v1)
[[0.3842]
 [2.4579]
 [2.7948]]

Note

The vectors do not have to be unit-length.

classmethod Rx(theta, unit='rad')[source]

Construct a new SO(3) from X-axis rotation

Parameters:

  • θ (float or array_like) – rotation angle about the X-axis

  • unit (str) – angular units: ‘rad’ [default], or ‘deg’

Returns:

SO(3) rotation

Return type:

SO3 instance

  • SE3.Rx(θ) is an SO(3) rotation of θ radians about the x-axis

  • SE3.Rx(θ, "deg") as above but θ is in degrees

If theta is an array then the result is a sequence of rotations defined by consecutive elements.

Example:

  File "<input>", line 1, in <module>
NameError: name 'x' is not defined
Traceback (most recent call last):
  File "<input>", line 1, in <module>
NameError: name 'x' is not defined
classmethod Ry(theta, unit='rad')[source]

Construct a new SO(3) from Y-axis rotation

Parameters:

  • θ (float or array_like) – rotation angle about Y-axis

  • unit (str) – angular units: ‘rad’ [default], or ‘deg’

Returns:

SO(3) rotation

Return type:

SO3 instance

  • SO3.Ry(θ) is an SO(3) rotation of θ radians about the y-axis

  • SO3.Ry(θ, "deg") as above but θ is in degrees

If θ is an array then the result is a sequence of rotations defined by consecutive elements.

Example:

  File "<input>", line 1, in <module>
NameError: name 'x' is not defined
Traceback (most recent call last):
  File "<input>", line 1, in <module>
NameError: name 'x' is not defined
classmethod Rz(theta, unit='rad')[source]

Construct a new SO(3) from Z-axis rotation

Parameters:

  • θ (float or array_like) – rotation angle about Z-axis

  • unit (str) – angular units: ‘rad’ [default], or ‘deg’

Returns:

SO(3) rotation

Return type:

SO3 instance

  • SO3.Rz(θ) is an SO(3) rotation of θ radians about the z-axis

  • SO3.Rz(θ, "deg") as above but θ is in degrees

If θ is an array then the result is a sequence of rotations defined by consecutive elements.

Example:

  File "<input>", line 1, in <module>
NameError: name 'x' is not defined
Traceback (most recent call last):
  File "<input>", line 1, in <module>
NameError: name 'x' is not defined
classmethod TwoVectors(x=None, y=None, z=None)[source]

Construct a new SO(3) from any two vectors

Parameters:

  • x (str, array_like(3), optional) – new x-axis, defaults to None

  • y (str, array_like(3), optional) – new y-axis, defaults to None

  • z (str, array_like(3), optional) – new z-axis, defaults to None

Return type:

Self

Create a rotation by defining the direction of two of the new axes in terms of the old axes. Axes are denoted by strings "x", "y", "z", "-x", "-y", "-z".

The directions can also be specified by 3-element vectors. If the vectors are not orthogonal, they will orthogonalized w.r.t. the first available dimension. I.e. if x is available, it will be normalized and the remaining vector will be orthogonalized w.r.t. x, else, y will be normalized and z will be orthogonalized w.r.t. y.

To create a rotation where the new frame has its x-axis in -z-direction of the previous frame, and its z-axis in the x-direction of the previous frame is:

>>> SO3.TwoVectors(x='-z', z='x')
UnitQuaternion()[source]

SO3 as a unit quaternion instance

Returns:

a unit quaternion representation

Return type:

UnitQuaternion instance

R.UnitQuaternion() is an UnitQuaternion instance representing the same rotation as the SO3 rotation R.

Example:

>>> from spatialmath import SO3
>>> SO3.Rz(0.3).UnitQuaternion()
UnitQuaternion(array([0.9888, 0.    , 0.    , 0.1494]))
__add__(right)

Overloaded + operator (superclass method)

Returns:

Sum of two operands

Return type:

NumPy array, shape=(N,N)

Raises:

ValueError – for incompatible arguments

Add the elements of two poses. This is not a group operation so the result is a matrix not a pose class.

  • X + Y is the element-wise sum of the matrix value of X and Y

  • X + s is the element-wise sum of the matrix value of X and scalar s

  • s + X is the element-wise sum of the scalar s and the matrix value of X

Operands

Sum

left

right

type

operation

Pose

Pose

NxN matrix

element-wise matrix sum

Pose

scalar

NxN matrix

element-wise sum

scalar

Pose

NxN matrix

element-wise sum

Note

  1. Pose is an SO2, SE2, SO3 or SE3 instance

  2. N is 2 for SO2, SE2; 3 for SO3 or SE3

  3. scalar + Pose is handled by __radd__()

  4. Addition is commutative

  5. Any other input combinations result in a ValueError.

For pose addition either or both operands may hold more than one value which results in the sum holding more than one value according to:

len(left)

len(right)

len

operation

1

1

1

sum = left + right

1

M

M

sum[i] = left + right[i]

N

1

M

sum[i] = left[i] + right

M

M

M

sum[i] = left[i] + right[i]
__eq__(right)

Overloaded == operator (superclass method)

Returns:

Equality of two operands

Return type:

bool or list of bool

Test two poses for equality

X == Y is true of the poses are of the same type and numerically equal.

If either or both operands may hold more than one value which results in the equality test holding more than one value according to:

len(left)

len(right)

len

operation

1

1

1

eq = left == right

1

M

M

eq[i] = left == right[i]

N

1

M

eq[i] = left[i] == right

M

M

M

eq[i] = left[i] == right[i]
__init__(arg=None, *, check=True)[source]

Construct new SO(3) object

Return type:

SO3 instance

There are multiple call signatures:

  • SO3() is an SO3 instance with one value – a 3x3 identity matrix which corresponds to a null rotation

  • SO3(R) is an SO3 instance with with the value R which is a 3x3 numpy array representing an SO(3) rotation matrix. If check is True check the matrix belongs to SO(3).

  • SO3([R1, R2, ... RN]) is an SO3 instance wwith N values given by the elements Ri each of which is a 3x3 NumPy array representing an SO(3) matrix. If check is True check the matrix belongs to SO(3).

  • SO3([X1, X2, ... XN]) is an SO3 instance with N values given by the elements Xi each of which is an SO3 or SE3 instance.

SymPy:

supported

__mul__(right)

Overloaded * operator (superclass method)

Returns:

Product of two operands

Return type:

Pose instance or NumPy array

Raises:

NotImplemented – for incompatible arguments

Pose composition, scaling or vector transformation:

  • X * Y compounds the poses X and Y

  • X * s performs element-wise multiplication of the elements of X by s

  • s * X performs element-wise multiplication of the elements of X by s

  • X * v linear transformation of the vector v where v is array-like

Multiplicands

Product

left

right

type

operation

Pose

Pose

Pose

matrix product

Pose

scalar

NxN matrix

element-wise product

scalar

Pose

NxN matrix

element-wise product

Pose

N-vector

N-vector

vector transform

Pose

NxM matrix

NxM matrix

transform each column

Note

  1. Pose is an SO2, SE2, SO3 or SE3 instance

  2. N is 2 for SO2, SE2; 3 for SO3 or SE3

  3. Scalar x Pose is handled by __rmul__`

  4. Scalar multiplication is commutative but the result is not a group operation so the result will be a matrix

  5. Any other input combinations result in a ValueError.

For pose composition either or both operands may hold more than one value which results in the composition holding more than one value according to:

len(left)

len(right)

len

operation

1

1

1

prod = left * right

1

M

M

prod[i] = left * right[i]

N

1

M

prod[i] = left[i] * right

M

M

M

prod[i] = left[i] * right[i]

Example:

>>> SE3.Rx(pi/2) * SE3.Ry(pi/2)
SE3(array([[0., 0., 1., 0.],
        [1., 0., 0., 0.],
        [0., 1., 0., 0.],
        [0., 0., 0., 1.]]))
>>> SE3.Rx(pi/2) * 2
array([[ 2.0000000e+00,  0.0000000e+00,  0.0000000e+00,  0.0000000e+00],
       [ 0.0000000e+00,  1.2246468e-16, -2.0000000e+00,  0.0000000e+00],
       [ 0.0000000e+00,  2.0000000e+00,  1.2246468e-16,  0.0000000e+00],
       [ 0.0000000e+00,  0.0000000e+00,  0.0000000e+00,  2.0000000e+00]])

For vector transformation there are three cases:

Multiplicands

Product

len(left)

right.shape

shape

operation

1

(N,)

(N,)

vector transformation

M

(N,)

(N,M)

vector transformations

1

(N,M)

(N,M)

column transformation

Note

  • The vector is an array-like, a 1D NumPy array or a list/tuple

  • For the SE2 and SE3 case the vectors are converted to homogeneous form, transformed, then converted back to Euclidean form.

Example:

>>> SE3.Rx(pi/2) * [0, 1, 0]
array([0.000000e+00, 6.123234e-17, 1.000000e+00])
>>> SE3.Rx(pi/2) * np.r_[0, 0, 1]
array([ 0.000000e+00, -1.000000e+00,  6.123234e-17])
__ne__(right)

Overloaded != operator (superclass method)

Returns:

Inequality of two operands

Return type:

bool or list of bool

Test two poses for inequality

  • X != Y is true of the poses are of the same type but not numerically equal.

If either or both operands may hold more than one value which results in the inequality test holding more than one value according to:

len(left)

len(right)

len

operation

1

1

1

ne = left != right

1

M

M

ne[i] = left != right[i]

N

1

M

ne[i] = left[i] != right

M

M

M

ne[i] = left[i] != right[i]
__pow__(n)

Overloaded ** operator (superclass method)

Parameters:

n (int) – exponent

Returns:

pose to the power n

Return type:

pose instance

X**n raise all values held in X to the specified power using repeated multiplication. If n < 0 then the result is inverted.

Example:

>>> from spatialmath import SE3
>>> SE3.Rx(0.1) ** 2
SE3(array([[ 1.    ,  0.    ,  0.    ,  0.    ],
           [ 0.    ,  0.9801, -0.1987,  0.    ],
           [ 0.    ,  0.1987,  0.9801,  0.    ],
           [ 0.    ,  0.    ,  0.    ,  1.    ]]))
>>> SE3.Rx([0, 0.1]) ** 2
SE3([
array([[1., 0., 0., 0.],
       [0., 1., 0., 0.],
       [0., 0., 1., 0.],
       [0., 0., 0., 1.]]),
array([[ 1.    ,  0.    ,  0.    ,  0.    ],
       [ 0.    ,  0.9801, -0.1987,  0.    ],
       [ 0.    ,  0.1987,  0.9801,  0.    ],
       [ 0.    ,  0.    ,  0.    ,  1.    ]]) ])
__sub__(right)

Overloaded - operator (superclass method)

Returns:

Difference of two operands

Return type:

NumPy array, shape=(N,N)

Raises:

ValueError – for incompatible arguments

Subtract elements of two poses. This is not a group operation so the result is a matrix not a pose class.

  • X - Y is the element-wise difference of the matrix value of X and Y

  • X - s is the element-wise difference of the matrix value of X and the scalar s

  • s - X is the element-wise difference of the scalar s and the matrix value of X

Operands

Sum

left

right

type

operation

Pose

Pose

NxN matrix

element-wise matrix difference

Pose

scalar

NxN matrix

element-wise sum

scalar

Pose

NxN matrix

element-wise sum

Note

  1. Pose is SO2, SE2, SO3 or SE3 instance

  2. N is 2 for SO2, SE2; 3 for SO3 or SE3

  3. scalar - Pose is handled by __rsub__()

  4. Any other input combinations result in a ValueError.

For pose subtraction either or both operands may hold more than one value which results in the difference holding more than one value according to:

len(left)

len(right)

len

operation

1

1

1

diff = left - right

1

M

M

diff[i] = left - right[i]

N

1

M

diff[i] = left[i] - right

M

M

M

diff[i] = left[i]  right[i]
__truediv__(right)

Overloaded / operator (superclass method)

Returns:

Product of right operand and inverse of left operand

Return type:

pose instance or NumPy array

Raises:

ValueError – for incompatible arguments

Pose composition or scaling:

  • X / Y compounds the poses X and Y.inv()

  • X / s performs elementwise division of the elements of X by s

Multiplicands

Quotient

left

right

type

operation

Pose

Pose

Pose

matrix product by inverse

Pose

scalar

NxN matrix

element-wise division

Note

  1. Pose is SO2, SE2, SO3 or SE3 instance

  2. N is 2 for SO2, SE2; 3 for SO3 or SE3

  3. Scalar multiplication is not a group operation so the result will be a matrix

  4. Any other input combinations result in a ValueError.

For pose composition either or both operands may hold more than one value which results in the composition holding more than one value according to:

len(left)

len(right)

len

operation

1

1

1

quo = left * right.inv()

1

M

M

quo[i] = left * right[i].inv()

N

1

M

quo[i] = left[i] * right.inv()

M

M

M

quo[i] = left[i] * right[i].inv()
angdist(other, metric=6)[source]

Angular distance metric between rotations

Parameters:

  • other (SO3 instance) – second rotation

  • metric (int) – metric, default is 6

Raises:

TypeError – if other is not an SO3

Returns:

angle in radians

Return type:

float or ndarray

R1.angdist(R2) is the geodesic norm, or geodesic distance between two rotations.

Several metrics are supported, the first 5 are computed after conversion to unit quaternions.

Metric

Details

0

\(1 - | \q_1 \bullet \q_2 | \in [0, 1]\)

1

\(\cos^{-1} | \q_1 \bullet \q_2 | \in [0, \pi/2]\)

2

\(\cos^{-1} | \q_1 \bullet \q_2 | \in [0, \pi/2]\)

3

\(2 \tan^{-1} \| \q_1 - \q_2\| / \|\q_1 + \q_2\| \in [0, \pi/2]\)

4

\(\cos^{-1} \left( 2 (\q_1 \bullet \q_2)^2 - 1\right) \in [0, 1]\)

5

\(\|I - \mat{R}_1 \mat{R}_2^T\| \in [0, 2]\)

6

\(\|\log \mat{R}_1 \mat{R}_2^T\| \in [0, \pi]\)

Example:

>>> from spatialmath import SO3
>>> R1 = SO3.Rx(0.3)
>>> R2 = SO3.Ry(0.3)
>>> print(R1.angdist(R1))
0.0
>>> print(R1.angdist(R2))
0.4234654354756045

Note

  • metrics 1, 2, 4 can throw ValueError “math domain error” due to numeric errors which push the argument of acos() marginally outside its domain [0, 1].

  • metrics 2 and 3 are equivalent, but 3 is more robust

Seealso:

UnitQuaternion.angdist()

angvec(unit='rad')[source]

SO(3) or SE(3) as angle and rotation vector

Parameters:

unit (str) – angular units: ‘rad’ [default], or ‘deg’

Returns:

\((\theta, \hat{\bf v})\)

Return type:

float or ndarray(3)

x.angvec() is a tuple \((\theta, v)\) containing the rotation angle and a rotation axis.

By default the angle is in radians but can be changed setting unit=’deg’.

Note

  • If the input is SE(3) the translation component is ignored.

Example:

>>> from spatialmath import SO3
>>> R = SO3.Rx(0.3)
>>> R.angvec()
(0.3, array([1., 0., 0.]))
Seealso:

eulervec() AngVec() angvec() AngVec(), angvec2r()

animate(*args, start=None, **kwargs)

Plot pose object as an animated coordinate frame (superclass method)

Parameters:

  • start (same as self) – initial pose, defaults to null/identity

  • **kwargs – plotting options

Return type:

None

  • X.animate() displays the pose X as a coordinate frame moving from the origin in either 2D or 3D. There are many options, see the links below.

  • X.animate(*args, start=X1) displays the pose X as a coordinate frame moving from pose X1, in either 2D or 3D. There are many options, see the links below.

Example:

>>> X = SE3.Rx(0.3)
>>> X.animate(frame='A', color='green')
>>> X.animate(start=SE3.Ry(0.2))
Seealso:

tranimate(), tranimate2()

append(item)

Append a value to an instance (BasePoseList superclass method)

Parameters:

x (Quaternion or UnitQuaternion instance) – the value to append

Raises:

ValueError – incorrect type of appended object

Return type:

None

Appends the argument to the object’s internal list of values.

Example:

>>> x = X.Alloc(10)
>>> len(x)
10
>>> x.append(X())   # append to the list
>>> len(x)
11

where X is any of the SMTB classes.

arghandler(arg, convertfrom=(), check=True)

Standard constructor support (BasePoseList superclass method)

Parameters:

  • arg (Any) – initial value

  • convertfrom (Tuple) – list of classes to accept and convert from

  • check (bool) – check value is valid, defaults to True

Type:

tuple of typles

Raises:

ValueError – bad type passed

Return type:

bool

The value arg can be any of:

  1. None, an identity value is created

  2. a numpy.ndarray of the appropriate shape and value which is valid for the subclass

  3. a list whose elements all meet the criteria above

  4. an instance of the subclass

  5. a list whose elements are all singelton instances of the subclass

For cases 2 and 3, a NumPy array or a list of NumPy array is passed. Each NumPyarray is tested for validity (if check is False a cursory check of shape is made, if check is True the numerical value is inspected) and converted to the required internal format by the _import method. The default _import method calls the isvalid method for checking. This mechanism allows equivalent forms to be passed, ie. 6x1 or 4x4 for an se(3).

If self is an instance of class A, and an instance of class B is passed and B is an element of the convertfrom argument, then B.A() will be invoked to perform the type conversion.

Examples:

SE3()
SE3(np.identity(4))
SE3([np.identity(4), np.identity(4)])
SE3(SE3())
SE3([SE3(), SE3()])
Twist3(SE3())
binop(right, op, op2=None, list1=True)

Perform binary operation

Parameters:

  • left (BasePoseList subclass) – left operand

  • right (BasePoseList subclass, scalar or array) – right operand

  • op (callable) – binary operation

  • op2 (callable) – binary operation

  • list1 (bool) – return single array as a list, default True

Raises:

ValueError – arguments are not compatible

Returns:

list of values

Return type:

list

The is a helper method for implementing binary operation with overloaded operators such as X * Y where X and Y are both subclasses of BasePoseList. Each operand has a list of one or more values and this methods computes a list of result values according to:

Inputs

Output

len(left)

len(right)

len

operation

1

1

1

ret = op(left, right)

1

M

M

ret[i] = op(left, right[i])

M

1

M

ret[i] = op(left[i], right)

M

M

M

ret[i] = op(left[i], right[i])

The arguments to op are the internal numeric values, ie. as returned by the ._A property.

The result is always a list, except for the first case above and list1 is False.

If the right operand is not a BasePoseList subclass, but is a numeric scalar or array then then op2 is invoked

For example:

X._binop(Y, lambda x, y: x + y)

Input

Output

len(left)

len

operation

1

1

ret = op2(left, right)

M

M

ret[i] = op2(left[i], right)

There is no check on the shape of right if it is an array. The result is always a list, except for the first case above and list1 is False.

clear() → None -- remove all items from S
conjugation(A)

Matrix conjugation

Parameters:

A (ndarray) – matrix to conjugate

Returns:

conjugated matrix

Return type:

ndarray

Compute the conjugation \(\mat{X} \mat{A} \mat{X}^{-1}\) where \(\mat{X}\) is the current object.

Example:

>>> from spatialmath import SO2
>>> import numpy as np
>>> R = SO2(0.5)
>>> A = np.array([[10, 0], [0, 1]])
>>> print(R * A * R.inv())
[[7.9314 3.7866]
 [3.7866 3.0686]]
>>> print(R.conjugation(A))
[[7.9314 3.7866]
 [3.7866 3.0686]]
det()

Determinant of rotational component (superclass method)

Returns:

Determinant of rotational component

Return type:

float or NumPy array

x.det() is the determinant of the rotation component of the values of x.

Example:

>>> x=SE3.Rand()
>>> x.det()
1.0000000000000004
>>> x=SE3.Rand(N=2)
>>> x.det()
[0.9999999999999997, 1.0000000000000002]
SymPy:

not supported

eul(unit='rad', flip=False)[source]

SO(3) or SE(3) as Euler angles

Parameters:

unit (str) – angular units: ‘rad’ [default], or ‘deg’

Returns:

3-vector of Euler angles

Return type:

ndarray(3,), ndarray(n,3)

x.eul is the Euler angle representation of the rotation. Euler angles are a 3-vector \((\phi, \theta, \psi)\) which correspond to consecutive rotations about the Z, Y, Z axes respectively.

If len(x) is:

  • 1, return an ndarray with shape=(3,)

  • N>1, return ndarray with shape=(3,N)

Seealso:

Eul(), tr2eul()

SymPy:

not supported

eulervec()[source]

SO(3) or SE(3) as Euler vector (exponential coordinates)

Returns:

\(\theta \hat{\bf v}\)

Return type:

ndarray(3)

x.eulervec() is the Euler vector (or exponential coordinates) which is related to angle-axis notation and is the product of the rotation angle and the rotation axis.

Example:

>>> from spatialmath import SO3
>>> R = SO3.Rx(0.3)
>>> R.eulervec()
array([0.3, 0. , 0. ])

Note

  • If the input is SE(3) the translation component is ignored.

Seealso:

angvec() angvec2r()

extend(iterable)

Extend sequence of values in an instance (BasePoseList superclass method)

Parameters:

x (instance of same type) – the value to extend

Raises:

ValueError – incorrect type of appended object

Return type:

None

Appends the argument’s values to the object’s internal list of values.

Example:

>>> x = X.Alloc(10)
>>> len(x)
10
>>> x.append(X.Alloc(5))   # extend the list
>>> len(x)
15

where X is any of the SMTB classes.

insert(i, item)

Insert a value to an instance (BasePoseList superclass method)

Parameters:

  • i (int) – element to insert value before

  • item (instance of same type) – the value to insert

Raises:

ValueError – incorrect type of inserted value

Return type:

None

Inserts the argument into the object’s internal list of values.

Example:

>>> x = X.Alloc(10)
>>> len(x)
10
>>> x.insert(0, X())   # insert at start of list
>>> len(x)
11
>>> x.insert(10, X())   # append to the list
>>> len(x)
11

where X is any of the SMTB classes.

Note

If i is beyond the end of the list, the item is appended to the list

interp(end=None, s=None, shortest=True)

Interpolate between poses (superclass method)

Parameters:

  • end (same as self) – final pose

  • s (array_like or int) – interpolation coefficient, range 0 to 1, or number of steps

  • shortest (bool, default to True) – take the shortest path along the great circle for the rotation

Returns:

interpolated pose

Return type:

same as self

  • X.interp(Y, s) interpolates pose between X between when s=0 and Y when s=1.

  • X.interp(Y, N) interpolates pose between X and Y in N steps.

Example:

>>> x = SE3(-1, -2, 0) * SE3.Rx(-0.3)
>>> y = SE3(1, 2, 0) * SE3.Rx(0.3)
>>> x.interp(y, 0)    # this is x
SE3(array([[ 1.    ,  0.    ,  0.    , -1.    ],
           [ 0.    ,  0.9553,  0.2955, -2.    ],
           [ 0.    , -0.2955,  0.9553,  0.    ],
           [ 0.    ,  0.    ,  0.    ,  1.    ]]))
>>> x.interp(y, 1)    # this is y
SE3(array([[ 1.    ,  0.    ,  0.    ,  1.    ],
           [ 0.    ,  0.9553, -0.2955,  2.    ],
           [ 0.    ,  0.2955,  0.9553,  0.    ],
           [ 0.    ,  0.    ,  0.    ,  1.    ]]))
>>> x.interp(y, 0.5)  # this is in between
SE3(array([[1., 0., 0., 0.],
           [0., 1., 0., 0.],
           [0., 0., 1., 0.],
           [0., 0., 0., 1.]]))
>>> z = x.interp(y, 11)  # in 11 steps
>>> len(z)
11
>>> z[0]              # this is x
SE3(array([[ 1.    ,  0.    ,  0.    , -1.    ],
           [ 0.    ,  0.9553,  0.2955, -2.    ],
           [ 0.    , -0.2955,  0.9553,  0.    ],
           [ 0.    ,  0.    ,  0.    ,  1.    ]]))
>>> z[5]              # this is in between
SE3(array([[1., 0., 0., 0.],
           [0., 1., 0., 0.],
           [0., 0., 1., 0.],
           [0., 0., 0., 1.]]))

Note

  • For SO3 and SE3 rotation is interpolated using quaternion spherical linear interpolation (slerp).

  • Values of s outside the range [0,1] are silently clipped

Seealso:

interp1(), trinterp(), qslerp(), trinterp2()

SymPy:

not supported

interp1(s=None)

Interpolate pose (superclass method)

Parameters:

  • end (same as self) – final pose

  • s (array_like) – interpolation coefficient, range 0 to 1

Returns:

interpolated pose

Return type:

SO2, SE2, SO3, SE3 instance

  • X.interp(s) interpolates pose between identity when s=0, and X when s=1.

    len(X)

    len(s)

    len(result)

    Result

    1

    1

    1

    Y = interp(X, s)

    M

    1

    M

    Y[i] = interp(X[i], s)

    1

    M

    M

    Y[i] = interp(X, s[i])

Example:

>>> x = SE3.Rx(0.3)
>>> print(x.interp(0))
SE3(array([[1., 0., 0., 0.],
           [0., 1., 0., 0.],
           [0., 0., 1., 0.],
           [0., 0., 0., 1.]]))
>>> print(x.interp(1))
SE3(array([[ 1.        ,  0.        ,  0.        ,  0.        ],
           [ 0.        ,  0.95533649, -0.29552021,  0.        ],
           [ 0.        ,  0.29552021,  0.95533649,  0.        ],
           [ 0.        ,  0.        ,  0.        ,  1.        ]]))
>>> y = x.interp(x, np.linspace(0, 1, 10))
>>> len(y)
10
>>> y[5]
SE3(array([[ 1.        ,  0.        ,  0.        ,  0.        ],
           [ 0.        ,  0.98614323, -0.16589613,  0.        ],
           [ 0.        ,  0.16589613,  0.98614323,  0.        ],
           [ 0.        ,  0.        ,  0.        ,  1.        ]]))

Notes:

  1. For SO3 and SE3 rotation is interpolated using quaternion spherical linear interpolation (slerp).

Seealso:

interp(), trinterp(), qslerp(), trinterp2()

SymPy:

not supported

inv()[source]

Inverse of SO(3)

Returns:

inverse

Return type:

SO2 instance

Efficiently compute the inverse of each of the SO(3) values taking into account the matrix structure. For an SO(3) matrix the inverse is the transpose.

ishom()

Test if object belongs to SE(3) group (superclass method)

Returns:

True if object is instance of SE3

Return type:

bool

For compatibility with Spatial Math Toolbox for MATLAB. In Python use isinstance(x, SE3).

Example:

>>> x = SO3()
>>> x.isrot()
False
>>> x = SE3()
>>> x.isrot()
True
ishom2()

Test if object belongs to SE(2) group (superclass method)

Returns:

True if object is instance of SE2

Return type:

bool

For compatibility with Spatial Math Toolbox for MATLAB. In Python use isinstance(x, SE2).

Example:

>>> x = SO2()
>>> x.isrot()
False
>>> x = SE2()
>>> x.isrot()
True
isrot()

Test if object belongs to SO(3) group (superclass method)

Returns:

True if object is instance of SO3

Return type:

bool

For compatibility with Spatial Math Toolbox for MATLAB. In Python use isinstance(x, SO3).

Example:

>>> x = SO3()
>>> x.isrot()
True
>>> x = SE3()
>>> x.isrot()
False
isrot2()

Test if object belongs to SO(2) group (superclass method)

Returns:

True if object is instance of SO2

Return type:

bool

For compatibility with Spatial Math Toolbox for MATLAB. In Python use isinstance(x, SO2).

Example:

>>> x = SO2()
>>> x.isrot()
True
>>> x = SE2()
>>> x.isrot()
False
static isvalid(x, check=True)[source]

Test if matrix is valid SO(3)

Parameters:

x (numpy.ndarray) – matrix to test

Returns:

True if the matrix is a valid element of SO(3), ie. it is a 3x3 orthonormal matrix with determinant of +1.

Return type:

bool

Seealso:

isrot()

log(twist=False)

Logarithm of pose (superclass method)

Returns:

logarithm

Return type:

ndarray

Raises:

ValueError

An efficient closed-form solution of the matrix logarithm.

Input

Output

Pose

Shape

Structure

SO2

(2,2)

skew-symmetric SE2 (3,3) augmented skew-symmetric

SO3

(3,3)

skew-symmetric SE3 (4,4) augmented skew-symmetric

Example:

>>> x = SE3.Rx(0.3)
>>> y = x.log()
>>> y
array([[ 0. , -0. ,  0. ,  0. ],
       [ 0. ,  0. , -0.3,  0. ],
       [-0. ,  0.3,  0. ,  0. ],
       [ 0. ,  0. ,  0. ,  0. ]])
Seealso:

trlog2(),

trlog()

SymPy:

not supported

mean(tol=20)[source]

Mean of a set of rotations

Parameters:

tol (float, optional) – iteration tolerance in units of eps, defaults to 20

Returns:

the mean rotation

Return type:

SO3 instance.

Computes the Karcher mean of the set of rotations within the SO(3) instance.

References:
norm()

Normalize pose (superclass method)

Returns:

pose

Return type:

SO2, SE2, SO3, SE3 instance

  • X.norm() is an equivalent pose object but the rotational matrix part of all values has been adjusted to ensure it is a proper orthogonal matrix rotation.

Example:

>>> x = SE3()
>>> y = x.norm()
>>> y
SE3(array([[1., 0., 0., 0.],
           [0., 1., 0., 0.],
           [0., 0., 1., 0.],
           [0., 0., 0., 1.]]))

Notes:

  1. Only the direction of A vector (the z-axis) is unchanged.

  2. Used to prevent finite word length arithmetic causing transforms to become ‘unnormalized’.

Seealso:

trnorm(), trnorm2()

plot(*args, **kwargs)

Plot pose object as a coordinate frame (superclass method)

Parameters:

**kwargs – plotting options

Return type:

None

  • X.plot() displays the pose X as a coordinate frame in either 2D or 3D. There are many options, see the links below.

Example:

>>> X = SE3.Rx(0.3)
>>> X.plot(frame='A', color='green')

(Source code, png, hires.png, pdf)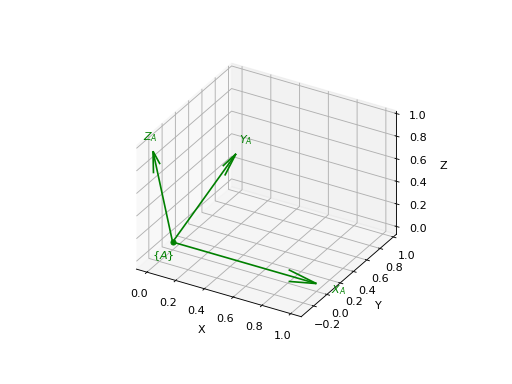

_images/3d_orient_SO3-1.png
Seealso:

trplot(), trplot2()

pop(i=-1)

Pop value from an instance (BasePoseList superclass method)

Parameters:

i (int) – item in the list to pop, default is last

Returns:

the popped value

Return type:

instance of same type

Raises:

IndexError – if there are no values to pop

Removes a value from the value list and returns it. The original instance is modified.

Example:

>>> x = X.Alloc(10)
>>> len(x)
10
>>> y = x.pop()  # pop the last value x[9]
>>> len(x)
9
>>> y = x.pop(0)  # pop the first value x[0]
>>> len(x)
8

where X is any of the SMTB classes.

print(label=None, file=None)

Print pose as a matrix (superclass method)

Parameters:

  • label (str, optional) – label to print before the matrix, defaults to None

  • file (file object, optional) – file to write to, defaults to None

Return type:

None

Print the pose as a matrix, with an optional line beforehand. By default the matrix is printed to stdout.

Example:

>>> from spatialmath import SE3
>>> SE3().print()
   1         0         0         0         
   0         1         0         0         
   0         0         1         0         
   0         0         0         1         

>>> SE3().print("pose is:")
pose is:
   1         0         0         0         
   0         1         0         0         
   0         0         1         0         
   0         0         0         1
Seealso:

printline() strline()

printline(*args, **kwargs)

Print pose in compact single line format (superclass method)

Parameters:

  • arg (str) – value for orient option, optional

  • label (str) – text label to put at start of line

  • fmt (str) – conversion format for each number as used by format()

  • label – text label to put at start of line

  • orient (str) – 3-angle convention to use, optional, SO3 and SE3 only

  • unit (str) – angular units: ‘rad’ [default], or ‘deg’

  • file (file object) – file to write formatted string to. [default, stdout]

Return type:

None

Print pose in a compact single line format. If X has multiple values, print one per line.

Orientation can be displayed in various formats:

orient

description

'rpy/zyx'

roll-pitch-yaw angles in ZYX axis order [default]

'rpy/yxz'

roll-pitch-yaw angles in YXZ axis order

'rpy/zyx'

roll-pitch-yaw angles in ZYX axis order

'eul'

Euler angles in ZYZ axis order

'angvec'

angle and axis

Example:

>>> from spatialmath import SE2, SE3
>>> x = SE3.Rx(0.3)
>>> x.printline()
t = 0, 0, 0; rpy/zyx = 17.2°, 0°, 0°
>>> x = SE3.Rx([0.2, 0.3])
>>> x.printline()
t = 0, 0, 0; rpy/zyx = 11.5°, 0°, 0°
t = 0, 0, 0; rpy/zyx = 17.2°, 0°, 0°
>>> x.printline('angvec')
t = 0, 0, 0; angvec = (11.5° | 1, 0, 0)
t = 0, 0, 0; angvec = (17.2° | 1, 0, 0)
>>> x.printline(orient='angvec', fmt="{:.6f}")
t = 0.000000, 0.000000, 0.000000; angvec = (11.459156° | 1.000000, 0.000000, 0.000000)
t = 0.000000, 0.000000, 0.000000; angvec = (17.188734° | 1.000000, 0.000000, 0.000000)
>>> x = SE2(1, 2, 0.3)
>>> x.printline()
t = 1, 2; 17.2°

Note

  • Default formatting is for compact display of data

  • For tabular data set fmt to a fixed width format such as fmt='{:.3g}'

Seealso:

strline() trprint(), trprint2()

prod(norm=False, check=True)

Product of elements (superclass method)

Parameters:

  • norm (bool, optional) – normalize the product, defaults to False

  • check – check that computed matrix is valid member of group, default True

Bool check:

bool, optional

Returns:

Product of elements

Return type:

pose instance

x.prod() is the product of the values held by x, ie. \(\prod_i^N T_i\).

>>> from spatialmath import SE3
>>> x = SE3.Rx([0, 0.1, 0.2, 0.3])
>>> x.prod()
SE3(array([[ 1.    ,  0.    ,  0.    ,  0.    ],
           [ 0.    ,  0.8253, -0.5646,  0.    ],
           [ 0.    ,  0.5646,  0.8253,  0.    ],
           [ 0.    ,  0.    ,  0.    ,  1.    ]]))

Note

When compounding many transformations the product may become denormalized resulting in a result that is not a proper member of the group. You can either disable membership checking by check=False which is risky, or normalize the result by norm=True.

reverse()

S.reverse() – reverse IN PLACE

rpy(unit='rad', order='zyx')[source]

SO(3) or SE(3) as roll-pitch-yaw angles

Parameters:

  • order (str) – angle sequence order, default to ‘zyx’

  • unit (str) – angular units: ‘rad’ [default], or ‘deg’

Returns:

3-vector of roll-pitch-yaw angles

Return type:

ndarray(3,), ndarray(n,3)

x.rpy is the roll-pitch-yaw angle representation of the rotation. The angles are a 3-vector \((r, p, y)\) which correspond to successive rotations about the axes specified by order:

  • 'zyx' [default], rotate by yaw about the z-axis, then by pitch about the new y-axis, then by roll about the new x-axis. Convention for a mobile robot with x-axis forward and y-axis sideways.

  • 'xyz', rotate by yaw about the x-axis, then by pitch about the new y-axis, then by roll about the new z-axis. Convention for a robot gripper with z-axis forward and y-axis between the gripper fingers.

  • 'yxz', rotate by yaw about the y-axis, then by pitch about the new x-axis, then by roll about the new z-axis. Convention for a camera with z-axis parallel to the optic axis and x-axis parallel to the pixel rows.

If len(x) is:

  • 1, return an ndarray with shape=(3,)

  • N>1, return ndarray with shape=(3,N)

Seealso:

RPY(), tr2rpy()

SymPy:

not supported

simplify()

Symbolically simplify matrix values (superclass method)

Returns:

pose with symbolic elements

Return type:

pose instance

Apply symbolic simplification to every element of every value in the pose instance.

Example:

>>> a = SE3.Rx(sympy.symbols('theta'))
>>> b = a * a
>>> b
SE3(array([[1, 0, 0, 0.0],
[0, -sin(theta)**2 + cos(theta)**2, -2*sin(theta)*cos(theta), 0],
[0, 2*sin(theta)*cos(theta), -sin(theta)**2 + cos(theta)**2, 0],
[0.0, 0, 0, 1.0]], dtype=object)
>>> b.simplify()
SE3(array([[1, 0, 0, 0],
[0, cos(2*theta), -sin(2*theta), 0],
[0, sin(2*theta), cos(2*theta), 0],
[0, 0, 0, 1.00000000000000]], dtype=object))
SymPy:

supported

stack()

Convert to 3-dimensional matrix

Returns:

3-dimensional NumPy array

Return type:

ndarray(n,n,m)

Converts the value to a 3-dimensional NumPy array where the values are stacked along the third axis. The first two dimensions are given by self.shape.

strline(*args, **kwargs)

Convert pose to compact single line string (superclass method)

Parameters:

  • label (str) – text label to put at start of line

  • fmt (str) – conversion format for each number as used by format()

  • label – text label to put at start of line

  • orient (str) – 3-angle convention to use, optional, SO3 and SE3 only

  • unit (str) – angular units: ‘rad’ [default], or ‘deg’

Returns:

pose in string format

Return type:

str

Convert pose in a compact single line format. If X has multiple values, the string has one pose per line.

Orientation can be displayed in various formats:

orient

description

'rpy/zyx'

roll-pitch-yaw angles in ZYX axis order [default]

'rpy/yxz'

roll-pitch-yaw angles in YXZ axis order

'rpy/zyx'

roll-pitch-yaw angles in ZYX axis order

'eul'

Euler angles in ZYZ axis order

'angvec'

angle and axis

Example:

>>> from spatialmath import SE2, SE3
>>> x = SE3.Rx(0.3)
>>> x.strline()
't = 0, 0, 0; rpy/zyx = 17.2°, 0°, 0°'
>>> x = SE3.Rx([0.2, 0.3])
>>> x.strline()
't = 0, 0, 0; rpy/zyx = 11.5°, 0°, 0°t = 0, 0, 0; rpy/zyx = 17.2°, 0°, 0°'
>>> x.strline('angvec')
't = 0, 0, 0; angvec = (11.5° | 1, 0, 0)t = 0, 0, 0; angvec = (17.2° | 1, 0, 0)'
>>> x.strline(orient='angvec', fmt="{:.6f}")
't = 0.000000, 0.000000, 0.000000; angvec = (11.459156° | 1.000000, 0.000000, 0.000000)t = 0.000000, 0.000000, 0.000000; angvec = (17.188734° | 1.000000, 0.000000, 0.000000)'
>>> x = SE2(1, 2, 0.3)
>>> x.strline()
't = 1, 2; 17.2°'

Note

  • Default formatting is for compact display of data

  • For tabular data set fmt to a fixed width format such as fmt='{:.3g}'

Seealso:

printline() trprint(), trprint2()

unop(op, matrix=False)

Perform unary operation

Parameters:

  • self (BasePoseList subclass) – operand

  • op (callable) – unnary operation

  • matrix (bool) – return array instead of list, default False

Returns:

operation results

Return type:

list or NumPy array

The is a helper method for implementing unary operations where the operand has multiple value. This method computes the value of the operation for all input values and returns the result as either a list or as a matrix which vertically stacks the results.

Input

Output

len(self)

len

operation

1

1

ret = op(self)

M

M

ret[i] = op(self[i])

M

M

ret[i,;] = op(self[i])

The result is:

  • a list of values if matrix==False, or

  • a 2D NumPy stack of values if matrix==True, it is assumed that the value is a 1D array.

property A: List[ndarray[Any, dtype[ScalarType]]] | ndarray[Any, dtype[ScalarType]]

Array value of an instance (BasePoseList superclass method)

Returns:

NumPy array value of this instance

Return type:

ndarray

  • X.A is a NumPy array that represents the value of this instance, and has a shape given by X.shape.

Note

This assumes that len(X) == 1, ie. it is a single-valued instance.

property N: int

Dimension of the object’s group (superclass property)

Returns:

dimension

Return type:

int

Dimension of the group is 2 for SO2 or SE2, and 3 for SO3 or SE3. This corresponds to the dimension of the space, 2D or 3D, to which these rotations or rigid-body motions apply.

Example:

>>> SE3().N
3
>>> SE2().N
2
property R: SO3Array

SO(3) or SE(3) as rotation matrix

Returns:

rotational component

Return type:

ndarray(3,3)

x.R is the rotation matrix component of x as an array with shape (3,3). If len(x) > 1, return an array with shape=(N,3,3).

Warning

The i’th rotation matrix is x[i,:,:] or simply x[i]. This is different to the MATLAB version where the i’th rotation matrix is x(:,:,i).

Example:

>>> from spatialmath import SO3
>>> x = SO3.Rx(0.3)
>>> x.R
array([[ 1.    ,  0.    ,  0.    ],
       [ 0.    ,  0.9553, -0.2955],
       [ 0.    ,  0.2955,  0.9553]])
SymPy:

supported

property a: ndarray[Any, dtype[floating]]

Approach vector of SO(3) or SE(3)

Returns:

approach vector

Return type:

ndarray(3)

This is the third column of the rotation submatrix, sometimes called the approach vector. It is parallel to the z-axis of the frame defined by this pose.

property about: str

Succinct summary of object type and length (superclass property)

Returns:

succinct summary

Return type:

str

Displays the type and the number of elements in compact form, for example:

>>> x = SE3([SE3() for i in range(20)])
>>> len(x)
20
>>> print(x.about)
SE3[20]
property isSE: bool

Test if object belongs to SE(n) group (superclass property)

Parameters:

self (SO2, SE2, SO3, SE3 instance) – object to test

Returns:

True if object is instance of SE2 or SE3

Return type:

bool

property isSO: bool

Test if object belongs to SO(n) group (superclass property)

Parameters:

self (SO2, SE2, SO3, SE3 instance) – object to test

Returns:

True if object is instance of SO2 or SO3

Return type:

bool

property n: ndarray[Any, dtype[floating]]

Normal vector of SO(3) or SE(3)

Returns:

normal vector

Return type:

ndarray(3)

This is the first column of the rotation submatrix, sometimes called the normal vector. It is parallel to the x-axis of the frame defined by this pose.

property o: ndarray[Any, dtype[floating]]

Orientation vector of SO(3) or SE(3)

Returns:

orientation vector

Return type:

ndarray(3)

This is the second column of the rotation submatrix, sometimes called the orientation vector. It is parallel to the y-axis of the frame defined by this pose.

property shape: Tuple[int, int]

Shape of the object’s interal matrix representation

Returns:

(3,3)

Return type:

tuple

Each value within the SO3 instance is a NumPy array of this shape.