2D ellipse
- class Ellipse(radii=None, E=None, centre=(0, 0), theta=None)[source]
- classmethod FromPerimeter(p)[source]
Create an ellipse that fits a set of perimeter points
- Parameters:
p (ndarray(2,N)) – a set of 2D perimeter points
- Returns:
an ellipse instance
- Return type:
Example:
>>> from spatialmath import Ellipse >>> import numpy as np >>> eref = Ellipse(radii=(1, 2), theta=np.pi / 4, centre=[3, 4]) >>> perim = eref.points() >>> print(perim.shape) (2, 20) >>> Ellipse.FromPerimeter(perim) Ellipse(radii=[1. 2.], centre=[3. 4.], theta=0.7853981633974318)
- Seealso:
- classmethod FromPoints(p)[source]
Create an equivalent ellipse from a set of interior points
- Parameters:
p (ndarray(2,N)) – a set of 2D interior points
- Returns:
an ellipse instance
- Return type:
Computes the ellipse that has the same inertia as the set of points.
- Seealso:
- classmethod Polynomial(e, p=None)[source]
Create an ellipse from polynomial
- Parameters:
e (arraylike(4) or arraylike(5)) – polynomial coeffients \(e\) or \(\eta\)
p (array_like(2), optional) – point to set scale
- Returns:
an ellipse instance
- Return type:
An ellipse can be specified by a polynomial \(\vec{e} \in \mathbb{R}^6\)
\[e_0 x^2 + e_1 y^2 + e_2 xy + e_3 x + e_4 y + e_5 = 0\]or \(\vec{\epsilon} \in \mathbb{R}^5\) where the leading coefficient is implicitly one
\[x^2 + \epsilon_1 y^2 + \epsilon_2 xy + \epsilon_3 x + \epsilon_4 y + \epsilon_5 = 0\]In this latter case, position, orientation and aspect ratio of the ellipse will be correct, but the overall scale of the ellipse is not determined. To correct this, we can pass in a single point
pthat we know lies on the perimeter of the ellipse.Example:
>>> from spatialmath import Ellipse >>> Ellipse.Polynomial([0.625, 0.625, 0.75, -6.75, -7.25, 24.625]) Ellipse(radii=[1. 2.], centre=[3. 4.], theta=0.7853981633974483)
- Seealso:
- __init__(radii=None, E=None, centre=(0, 0), theta=None)[source]
Create an ellipse
- Parameters:
radii (arraylike(2), optional) – radii of ellipse, defaults to None
E (ndarray(2,2), optional) – 2x2 matrix describing ellipse, defaults to None
centre (arraylike(2), optional) – centre of ellipse, defaults to (0, 0)
theta (float, optional) – orientation of ellipse, defaults to None
- Raises:
ValueError – bad parameters
The ellipse shape can be specified by
radiiandthetaor by a symmetric 2x2 matrixE.Internally the ellipse is represented by a symmetric matrix \(\mat{E} \in \mathbb{R}^{2\times 2}\) and its centre coordinate \(\vec{x}_0 \in \mathbb{R}^2\) such that
\[(\vec{x} - \vec{x}_0)^{\top} \mat{E} \, (\vec{x} - \vec{x}_0) = 1\]Example:
>>> from spatialmath import Ellipse >>> import numpy as np >>> Ellipse(radii=(1,2), theta=0) Ellipse(radii=[1. 2.], centre=(0, 0), theta=0.0) >>> Ellipse(E=np.array([[1, 1], [1, 2]])) Ellipse(radii=[1.618 0.618], centre=(0, 0), theta=1.0172219678978514)
- contains(p)[source]
Test if points are contained by ellipse
- Parameters:
p (arraylike(2), ndarray(2,N)) – point or points to test
- Returns:
true if point is contained within ellipse
- Return type:
bool or list(bool)
Example:
>>> from spatialmath import Ellipse >>> e = Ellipse(radii=(1,2), centre=(3,4), theta=0.5) >>> e.contains((3,4)) True >>> e.contains((0,0)) False
- plot(**kwargs)[source]
Plot ellipse
- Parameters:
kwargs – arguments passed to
plot_ellipse()- Returns:
list of artists
- Return type:
_type_
Example:
>>> from spatialmath import Ellipse >>> from spatialmath.base import plotvol2 >>> plotvol2(5) >>> e = Ellipse(E=np.array([[1, 1], [1, 2]])) >>> e.plot() >>> e.plot(filled=True, color='r')
(
Source code,png,hires.png,pdf)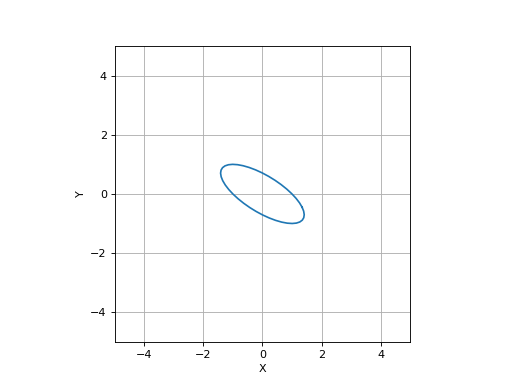
(
Source code,png,hires.png,pdf)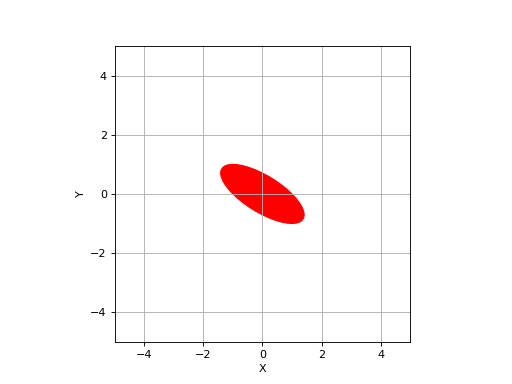
- Seealso:
- points(resolution=20)[source]
Generate perimeter points
- Parameters:
resolution (int, optional) – number of points on circumferance, defaults to 20
- Returns:
set of perimeter points
- Return type:
Points2
Return a set of
resolutionpoints on the perimeter of the ellipse. The perimeter set is not closed, that is, last point != first point.Example:
>>> from spatialmath import Ellipse >>> e = Ellipse(radii=(1,2), centre=(3,4), theta=0.5) >>> e.points()[:,:5] # first 5 points array([[4.2298, 4.0396, 3.7477, 3.3825, 2.9799], [3.5793, 4.1469, 4.7001, 5.1848, 5.5535]])
- Seealso:
polygon()ellipse()
- polygon(resolution=10)[source]
Approximate with a polygon
- Parameters:
resolution (int, optional) – number of polygon vertices, defaults to 20
- Returns:
a polygon approximating the ellipse
- Return type:
Polygon2instance
Return a polygon instance with
resolutionvertices. APolygon2`can be used for intersection testing with lines or other polygons.Example:
>>> from spatialmath import Ellipse >>> e = Ellipse(radii=(1,2), centre=(3,4), theta=0.5) >>> e.polygon() Polygon2 with 10 vertices
- Seealso:
- property E
Return ellipse matrix
- Returns:
ellipse matrix
- Return type:
ndarray(2,2)
The symmetric matrix \(\mat{E} \in \mathbb{R}^{2\times 2}\) determines the radii and the orientation of the ellipse
\[(\vec{x} - \vec{x}_0)^{\top} \mat{E} \, (\vec{x} - \vec{x}_0) = 1\]Example:
>>> from spatialmath import Ellipse >>> e = Ellipse(radii=(1,2), centre=(3,4), theta=0.5) >>> e.E array([[0.8276, 0.3156], [0.3156, 0.4224]])
- property area: float
Area of ellipse
- Returns:
area
- Return type:
float
Example:
>>> from spatialmath import Ellipse >>> e = Ellipse(radii=(1,2), centre=(3,4), theta=0.5) >>> e.area 6.283185307179586
- property centre: ndarray[Any, dtype[floating]]
Return ellipse centre
- Returns:
centre of the ellipse
- Return type:
ndarray(2)
Example:
>>> from spatialmath import Ellipse >>> e = Ellipse(radii=(1,2), centre=(3,4), theta=0.5) >>> e.centre (3, 4)
- property polynomial
Return ellipse as a polynomial
- Returns:
polynomial
- Return type:
ndarray(6)
An ellipse can be described by \(\vec{e} \in \mathbb{R}^6\) which are the coefficents of a quadratic in \(x\) and \(y\)
\[e_0 x^2 + e_1 y^2 + e_2 xy + e_3 x + e_4 y + e_5 = 0\]Example:
>>> from spatialmath import Ellipse >>> e = Ellipse(radii=(1,2), centre=(3,4), theta=0.5) >>> e.polynomial array([ 0.8276, 0.4224, 0.6311, -7.4901, -5.2724, 21.7799])
- Seealso: